What is a neural net anyway?
In early 2017, I was recovering from an illness and had some time on my hands. I like to learn new things (“smash myself into new ideas”) and the papers were full of articles about artificial intelligence. “Neural Nets” were mentioned all the time and I read that: “they mimic the workings of our brains”. It all sounded so amazing to me that I decided to take a deep dive into this brave new world.

In this blog, I’m going to try and explain what a neural net is and use simple examples to give some insight into how they work. It’s loosely part of my occasional series showing how ai can be used to solve real life problems. You definitely don’t need to be a data scientist or even a mathematician to understand. If you are reasonably numerate, that should be enough!
But why might it be a good thing for you to understand a little bit more about ai? Ai is everywhere and very, very few people understand what it is and how it can be used to create value in our organisations. The headlines tend to focus on the really big ticket projects like self driving cars and autonomous robots. In my experience, ai can generate value through application in far less exciting and more mundane domains. I’m hoping some readers of this blog (maybe you!) will use their new found understanding to draw back the veil of mystery and consider processes where automatic classification or anomaly detection could help to create value. Once that’s done, the next step is to start a conversation with colleagues and maybe IT professionals to consider how practical that application might be. The moment you take a single step down that route, you set yourself apart from the vast majority of managers, leaders and entrepreneurs. Your chances of creating value immediately increase. I’m sure it won’t be the easiest blog you’ve ever read, but I tried to lead you on a safe path to discovery!
I’ll be attacking the same problem from a number of directions to understand the difference between the way that we (with all our general intelligence) will solve a problem and the way that a neural net (with no general intelligence) will solve a problem.
So here is a nice simple problem that I first used with my son Chris when he was cramming for his Maths GCSE on the night before the actual exam!
Imagine that you go out with your friends in nearby Buckingham on Monday, Tuesday and Wednesday one week. You had a few ginger beers and got a taxi home that runs a strict fixed price per mile policy. When you wake up the following morning and your Mum asks you about your spending on the night out, your memory is a bit hazy and the details seem to escape you! You can’t remember the price of anything. Your Dad senses weakness and piles in to ask you how much your night out would cost if you drank 3 ginger beers and got a taxi home.
It shouldn’t be a hard question but how much the ginger beers were each and how much the taxi home was are lost in the mists of time.
By looking in your wallet, you know the following information:

So, how much would a night out with three ginger beers and a taxi cost?
Method 1: Intuition
If we look at the data we’ll notice quite quickly that the money spent is always one more pound than the number of drinks. Without hardly realising we’re doing it, we might take a guess that the taxi was £1 and that the drinks were also £1. Again, without realising it, we might do a quick calculation and confirm that the cost of £6 on Wednesday was indeed £1 for the taxi + £1 * 5 ginger beers.
So with a flourish, we can announce that the cost of our mythical night out would be £4
This method is very useful if the numbers are nice and round which of course they are in this example!
Problem solved!!!
Method 2: GCSE Maths
We might remember from helping with maths homework that this problem looks like:

Where y is the total cost of the evening, m is the cost of one ginger beer, x is the number of ginger beers consumed and c is the cost of the taxi.
We might remember that you can solve this type of problem graphically:
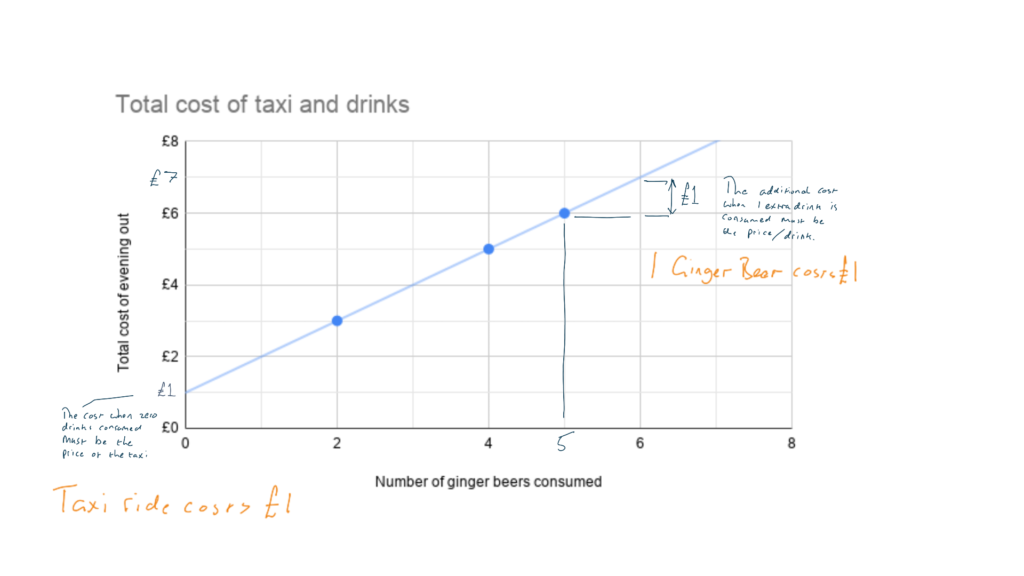
Again, we arrive at the same answer that our night out would cost £4.
This method works well even if our numbers have many decimal places.
We could also use our GCSE skills to solve it with simultaneous equations but I think we don’t need to do that here 🙂
Method 3: A Neural Net
If you’ve heard the expression “using a sledgehammer to crack a nut”, we’re way beyond that now!
This is more like “training a chef for ten years on the optimum method of using a sledgehammer to crack a nut so they can crack the nut and retrieve our kernel of nutty goodness!”
We didn’t learn about these things in GCSE Maths (or A Level for that matter), so I’ll try to go carefully.
Our brains are made of neurons and synapses. A neuron in our brain can take many input signals and decide how to combine them together and forward the result on. In our brains we have about 100 billion neurons. They are connected to each other by synapses that carry the signals into and out of the neurons. The number of synapses in our brain is really huge. They’re a bit difficult to count but the number is probably between 100 trillion and 1000 trillion. Those numbers are so huge, it’s difficult for us mere mortals to comprehend them.
If we had £100 trillion in a pile of £50 notes (with the picture of Alan Turing on them) the pile would be over 1,600 miles high!
So it’s a lot of synapses!
When we connect 100 Billion neurons together using 100 trillion synapses, we get an organic network of mind bending complexity.
When we stick our sensory organs (eyes, ears etc) to the front end of the network and our expressive facilities to the back end, then the possibilities are both astonishing and mundane. Every second of every day we use this system to observe, infer and communicate everything we need to survive and thrive.
We can use these concepts in our computers to solve problems and we call them Neural Nets. To calculate the cost of our night out with 3 ginger beers, we are going to use a much, much, much simpler neural net.
It will have two neurons (we call them perceptrons in the computing world). The input is the number of ginger beers consumed and the output is the total amount of money Chris spent on his night out.
I’ve created a diagram of the neural net to solve this problem below:
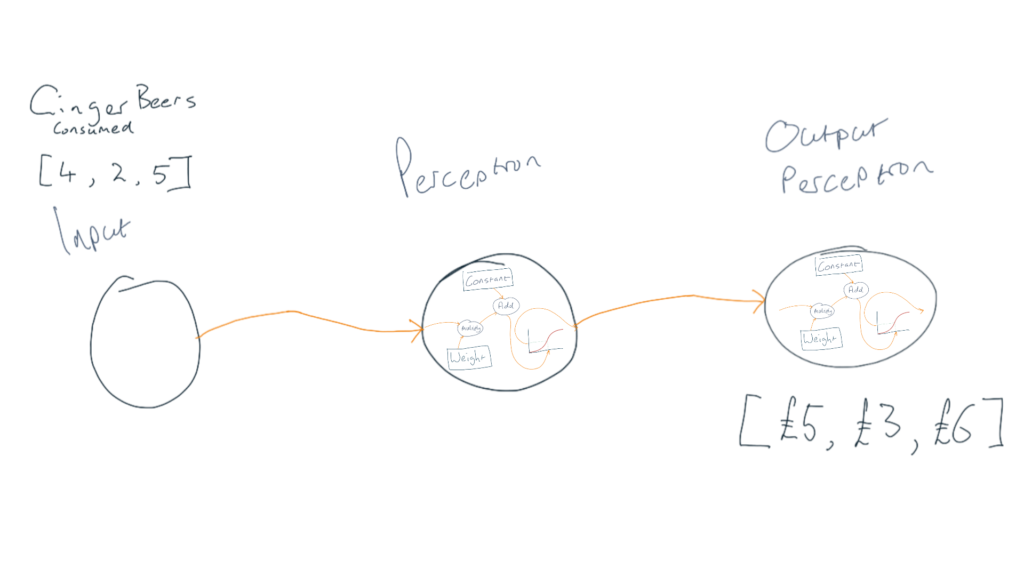
The input just contains a list of the number of ginger beers consumed on the nights out.
When our neural network is fully trained, the output perceptron spits out the costs that it calculated.
The magic happens in the two perceptrons (one in the middle and one on the right). The detail is too tiny for you to see so I’ve enlarged it below.
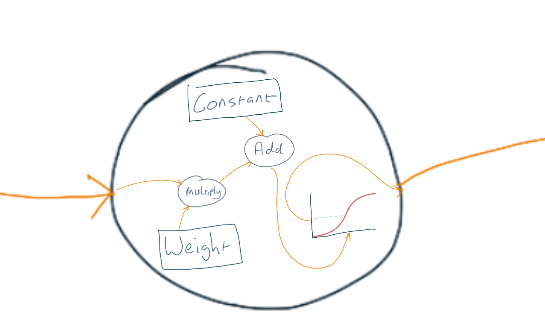
We only need one input on our perceptron to solve the ginger beer problem. But a perceptron can have many inputs. If we were doing something much more complicated, like reading handwritten letters, then there would be an input for each pixel of the image of the letters.
So what happens inside a perceptron?
- Each input is multiplied by its associated weight
- We add all those numbers together
- Then we add the constant weight
- Then we take that value and look it up on the horizontal axis of the graph
- Finally we read off the value on the vertical axis of the graph and send that to the output
We start at the left hand side of our network and repeat this process for every perceptron.
When we’ve calculated all the outputs, right up to the output perceptron, then we have our answer!
I’m sure that many of you will have spotted the “gotcha” in my description!
The output will be dependent on the value of the input AND the value of the constant AND all the weights in each perceptron!
We can find the correct constants and weights for all the perceptrons through a process called training. If we’re training, then it must be learning right? And if its learning then it must be intelligent? Well, that’s the general idea!
So how can we do the training?
Have you ever played the “I’m thinking of a number” game?
I think of a whole number and you have to guess what it is. Every time you make a guess, I tell you if my number is higher or lower than your guess. You keep tweaking your guess and eventually, you’ll be certain what my number is.
We could call that an” iterative process” and essentially, that’s how the training of our neural net works.
When we create the perceptrons we assign all the weights and constants a set of completely random numbers between -1 and +1.
The chances of those random weights being processed with the inputs as I described above and producing the correct result is as close to zero as makes no difference!
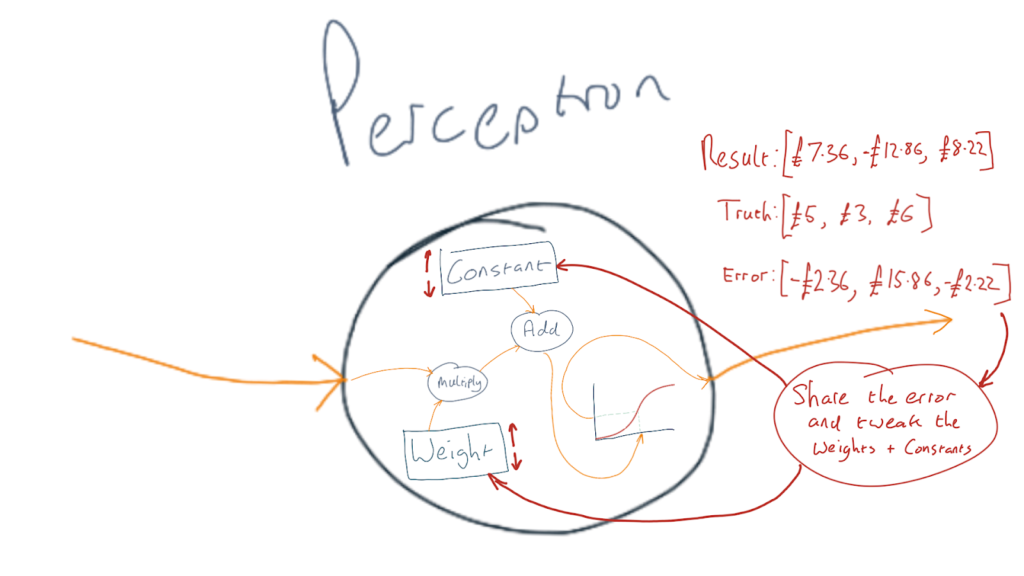
But…. They will produce a result. It’s just a guess in the beginning.
And just like in the “I’m thinking of a number” game, we can compare that guess to the “truth” to give us an “error”.
Once we’ve done that, we know if the weights and constants are too high or too low and how far off the target they are.
There’s a bit of maths that we can use to share the error out over the weights and constants in all the perceptrons and then just like in the “I’m thinking of a number” game, we will tweak the weights and constants up or down a little bit.
Then we repeat and keep doing so until our weights give us an answer that’s close enough to the truth for us to be happy!
I created this short animation of the training process

All that to calculate the price of a night out?!?
Well, what did you expect? 😉
I did say that we are deep behind the lines in overkill territory!
And…
In the world of computers, once we’ve written the code to create a perceptron, connect them together, do the weights allocation and the training as I described, we’ve broken the back of how to solve some really hard problems.
Computers can do all those things really, really, really quickly.
I get it – what about a more complex example?
I seem to hear you say! 😉
I defined a neural net with more complexity and trained it how to solve a sin curve. I chose this example because many people might remember the sin curve from their school days and it’s easy to generate the training data.
As a refresher, the graph in the chart below shows the sin curve in orange. The blue line is the output from the neural net before we’ve made any attempt to tweak the constants and weights in a training process. So at the beginning, the output looks nothing like the sin curve and our error will be huge.
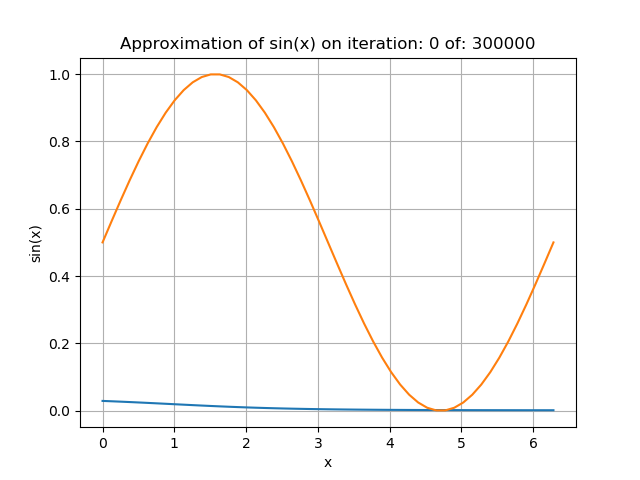
I created the visualisation below that should be playing continuously as you read the blog. It starts with a visualisation of the neural net I designed to solve the sin curve problem and then shows the output as it progresses through 300,000 training iterations.

I hope you can see that after the training is finished, the output from the neural net matches the actual sin curve pretty well.
Whilst this example is much more complex than the ginger beer problem, it’s still pretty pointless to be honest! Just about every computer language known is able to calculate the sin of an angle almost instantaneously. But it is a complex problem and we can see that the neural net can solve it as well, pretty easily.
Ok, not bad – what else can they do? Something useful perhaps?
When aspiring Data Scientists start to study neural nets, one of the traditional problems they have to solve is the decoding of handwritten digits into the numbers they represent.
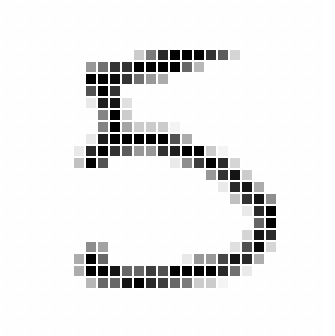
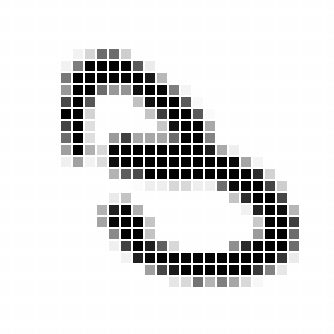
This hand drawn 5 and 3 are examples of the problem that needs to be solved. It’s in a matrix of 784 pixels (28 wide by 28 high).
I hope you can see that this is not a trivial problem to solve. If we had to try and work out the rules that would allow almost any hand drawn digit to be decoded, we would end up with an extremely long list of rules.
This is the type of problem where neural nets can excel. There are many inputs (784 pixels) and we can easily create the training data because almost anyone can look at a hand drawn digit and record what number it represents.
Luckily, some people have already done the tedious bit and there is a dataset of 50,000 hand drawn digits all provided with the known truth of what each one represents. Data scientists can then concentrate on designing a neural net and then training it to solve the problem. It’s one of the problems I solved myself in the summer of 2017 and you can see a live demonstration of my real time solution working here: (solving hand drawn digits)
Of course the neural net to solve these is a bit more complex than the “ginger beer” problem (and the sin curve). I created a visualisation of it to include here. However, it was so complex, with the lines packed so closely together, it was just a solid block of colour!
So I made the representation of a small portion of it with only 28 inputs instead of the full 784:

Green lines connect the inputs to the perceptrons and blue lines connect the perceptrons to the output perceptrons.
So, a neural net can read hand drawn digits, how about something that can actually make lives better?
Neural nets are incredibly useful when we have lots of inputs and many examples of those inputs where we know the truth. For example a retinal scan will contain millions of pixels and each one is a data point that a neural net can learn about when we provide it with the ”truth” of a diagnosis by a human expert.
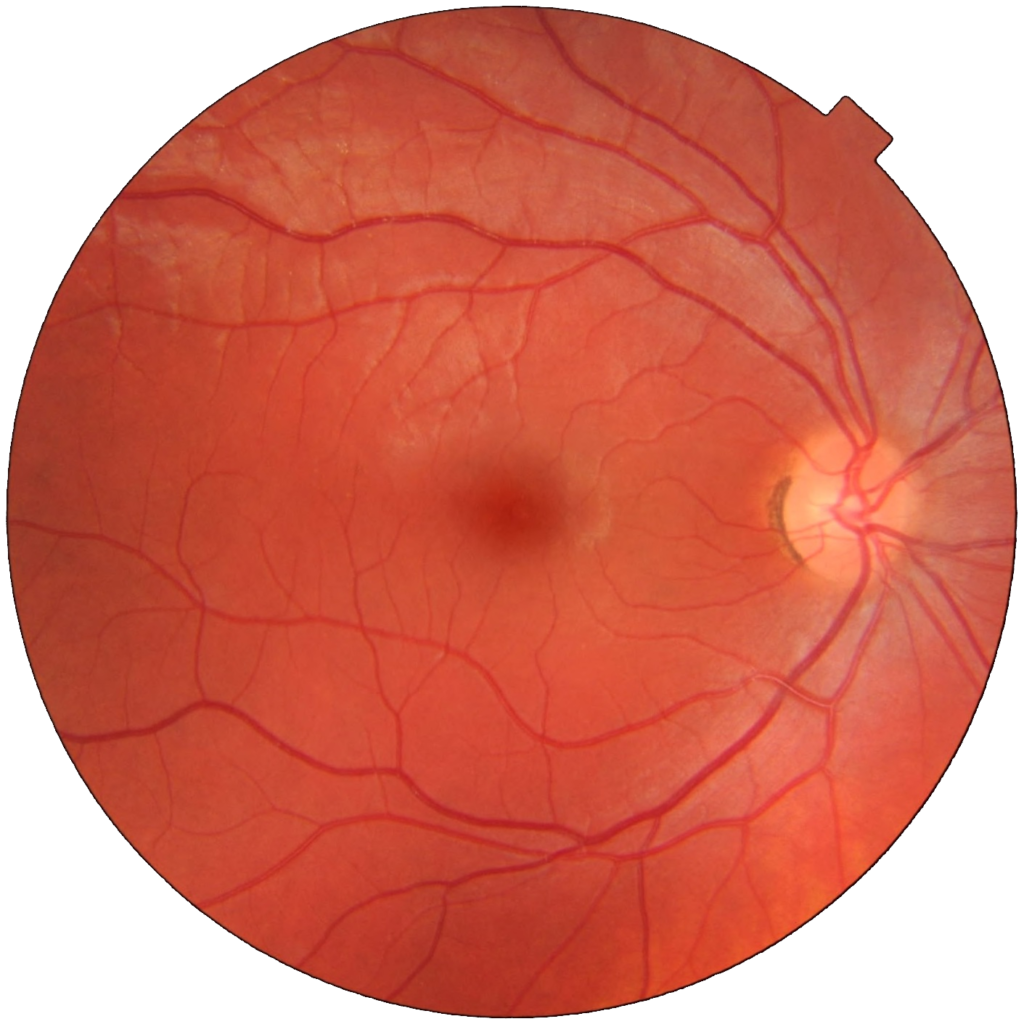
Häggström, Mikael (2014)
Neural nets have been designed and trained than can now outperform experienced medical professionals at interpreting retinal scans to diagnose conditions such as:
- Glaucoma
- Diabetes
- Macular degeneration
- Cancer
The neural nets for advanced image analysis have a few other fancy tricks to help but at the heart of all neural nets is a perceptron.
The perceptron has inputs, a weight for each of those inputs and a constant. It adds up the product of the weights and inputs then adds the constant to create a single number. It then converts that number by looking it up on a graph to create the output.
The output can be used as an input to other perceptrons and in this way, a neural net is created.
Finally (phew!)
I know this blog won’t be everyone’s cup of tea! Some may say that I have trivialised and glossed over some of the really important maths. Some may say it’s too complicated to follow.
I wanted to write this blog for the people who are numerate but not necessarily mathematicians and are curious about how things work and what they can do.
And whatever your background, if you got to here thanks very much for making the time and putting in the effort. If the concepts are new to you and you feel you understand the subject better than you did at the start then congratulations. You have successfully “smashed yourself into a new idea” and broadened your horizons. As a result, you’ve increased your ability to innovate and in almost all walks of life, that is a good skill to have. (if innovation is your thing, then you might enjoy another of my blogs: Five tools for innovation mastery)
Of course, not everyone will read this blog and go on to become Data Scientists, that wasn’t my intent. But as you try to solve problems that you face in business or life, sometimes it might help to consider the following points:
At the beginning, the neural net just guesses the weights and constants with random numbers then checks to see how far it’s answer is from the truth.
Sometimes, when we’re stuck between two choices and we can’t see a way to pick the best, we could just guess and pick one of them at random.
After a while (an iteration) we could go back and reconsider if any of our new information now throws new light on that decision.
Even after many hundreds of thousands of iterations, there is still a gap between the “truth” and the neural nets result. Perfection is our enemy. Working out when our solution is “good enough” is a key skill for successful managers, leaders and entrepreneurs.
If you’ve got your own tough business challenges and you think it might help to get some external perspective and challenge from experienced professionals then please give me a call 🙂
Peter Brookes-Smith
Curious problem solver, business developer, technologist and customer advocate
Other blogs by Peter
- Under the Tarpaulin Something Lurks
- Sign here…
- Legacy Applications – How did we get here and what can we do?
- Needles and haystacks or…
- The Case of Rev. Bayes v The Post Office
- Lighting a fire – Our first annual review…
- Helping Mine Detectors learn to use their equipment correctly
- How many?
- Finding defects with AI and computer vision
- Portfolio: PBS – Neural Net for Hand Written Digits
- CS50 – Harvard’s Open Computer Science Course
- Values Driven Business
- All things come to those that wait…
- Monte Carlo or Bust!
- What is business agility? And why should I care?
- Are values in business our fair weather friend?
- Lessons in life from an ai agent
- Five tools for innovation mastery
- Value for money
- Award entry for European CEO Magazine 2017
- Darwin and The Travelling Salesperson
- What is this DevOps thing?
Blogs by other authors:
- From Stubble to Squad Goals: Our Mo-numental Mo-vember Mo-arvel!
- Learning a Foreign Language vs. Learning to Code: What’s the Difference?
- Solving complex problems through code – and nature!
- In it together – why employee ownership is right for us
- Old Dogs and New Tricks: The Monte Carlo Forecasting Journey
- Portfolio: Rachel – Photo Editing
- Portfolio: Luke – Hangman
- Portfolio: Will – Gym Machines


