Darwin and The Travelling Salesperson

This is part of an occasional series taking a light hearted look at ai and how it can be applied to real world (sometimes!) situations.

If a salesperson has to visit all the cities in their patch and then return home every night, how could they work out the shortest route?

The Travelling Salesperson is a well known problem with many good methods for solving. Wikipedia has a lot of background info for the hungry!

But, to the point… I like to have a small project for my holidays (this year, it’s two weeks with most of our children and some of their friends / partners in Corfu).

I started to read an article a few weeks ago entitled “Evolution of a salesman: A complete genetic algorithm tutorial for Python”. Two sentences in, and I stopped.

Rightly or wrongly, I concluded that a genetic algorithm followed Darwinian principles and I decided to try and solve this problem myself without reading any more about it or looking at other people’s code. You may think it’s a ridiculous constraint, probably I agree 🙂

But it was an utterly delicious problem and I knew that it would consume me until I had it solved!

I’ve used Darwinian thinking many times before and I believe there are 3 conditions required for evolution to occur:

• Survival of the fittest
• Random variation
• Procreation with the offspring carrying forward some combination of the parents’ attributes

But hang on (I seem to hear my Old Dad say!), why bother with all that Darwinian complexity? It sounds pretty easy. Just work out all the routes and pick the shortest. Yes, there will be a lot of routes, but computers are fast. My Dad wouldn’t have known it, but that is called a Brute Force Strategy.

Well, it was also my first thought and if the number of cities is always small (say less than 15) then it might just about be viable. However, if the number of cities is 16, then the amount of routes that need calculating and checking is about 650 billion. And that is a pretty big number!

If we managed to calculate a million routes per second and then chose the shortest, we’d be running our program for about 8 days.

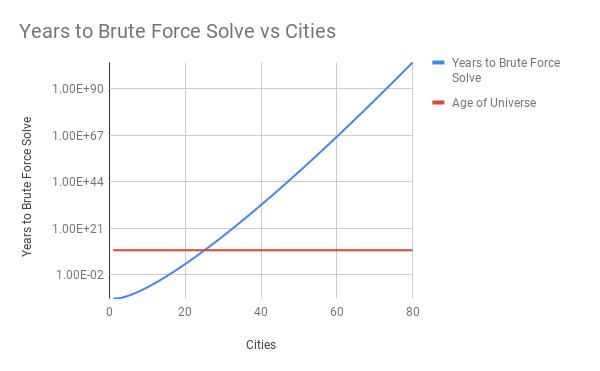
And it gets worse, if we have 26 cities, and managed to start calculating one million routes per second at the time of the big bang, we’d still be going now and it won’t complete for a good while yet!

70 cities and there are more possible routes than there are atoms in the universe!

Perfection is our enemy here and the pursuit of it, down the brute force road, leads us to a Herculean task (well, I am in Greece!).

We need to be smarter and evolution is pretty smart so I’ll take my lead from there.

A Darwinian Approach

For personal learning projects, Javascript and Python are my languages of choice. I decided to use Python with numpy, just because I wanted to!

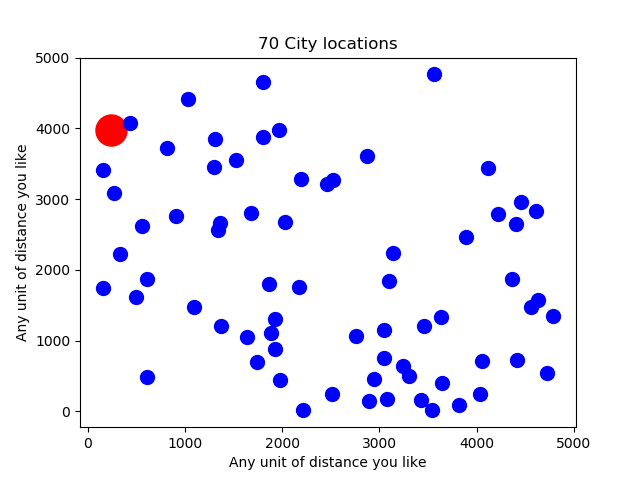
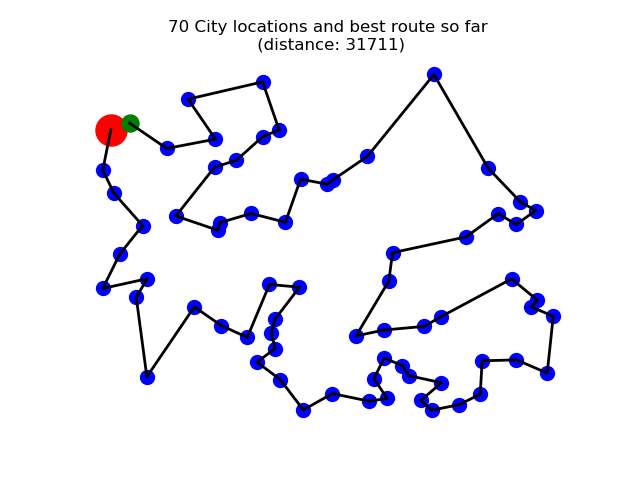
I started to build the world and solve the problem. First I needed to create a number of cities and plot them on a grid. I did that randomly rather than trying to specify a load of coordinates. Here’s a random map  with 70 Cities. My challenge is to find the shortest route for our poor sales person to visit each one and then return home (the large red blob).

Then I needed some potential routes. So I generated 2000 completely random ones and then calculated the total distance of each one.

They weren’t even close to optimal and the best one from that first batch is shown below:

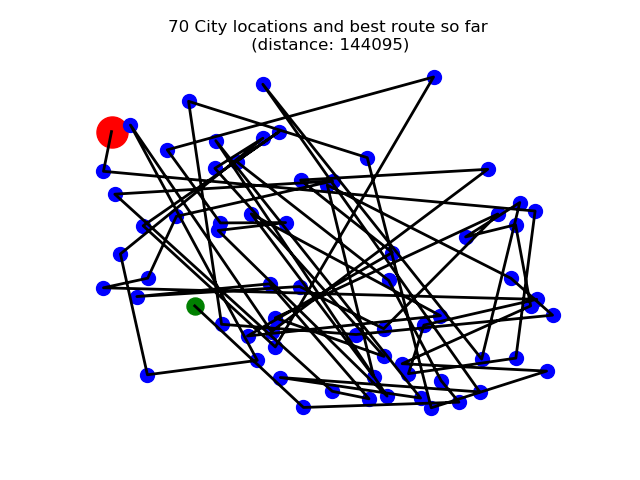
It starts at the red blob and the last city before returning home is the slightly hidden green blob.

Calculating the distance for 2000 routes is pretty quick on a computer so I did that and sorted my list of routes into order with the shortest being first.

Survival of the fittest

Before the bloodbath, I need to know how fit each route is. I wanted a number that is between zero and one for fitness so my best route had a fitness of one and my worst route (2000th) had a fitness of 1/2000 or 0.0005. Now the killing.

I didn’t create a threshold and kill everything below, rather I simulated some random danger and let nature decide. Each route faced its own danger and the dangerousness (!) was represented by a random number generated just for the purpose.  If the fitness of each route was less than the danger, it died.

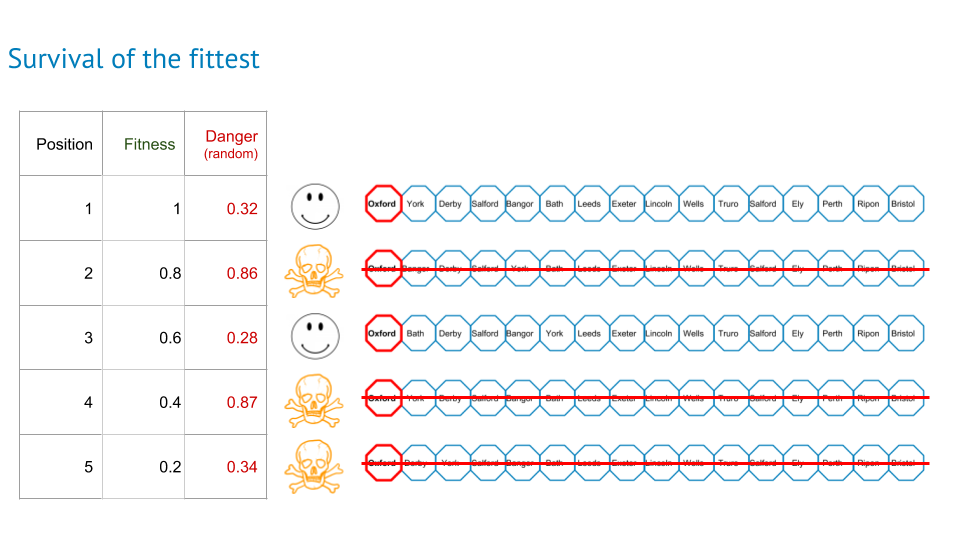
This meant that some pretty fit ones died and some pretty unfit ones survived but it seemed to reflect nature and who knows what important part a poorer quality route may have in the future. Anyway, that was my rule.

I tried a few different functions for generating the danger. In the end, I chose:

danger = 1 –  random_number * another_random_number

This danger function caused about three quarters of the routes to perish.

It was brutal!

Mutation

This was a bit trickier but not too bad! I worked through the routes that survived the danger. For each route to be mutated, I chose a random number of route mutations (between one and the number of cities) and then randomly picked that many pairs of cities (in the example below, there are three mutations for that route). The last act was to swap the position of those pairs of cities.

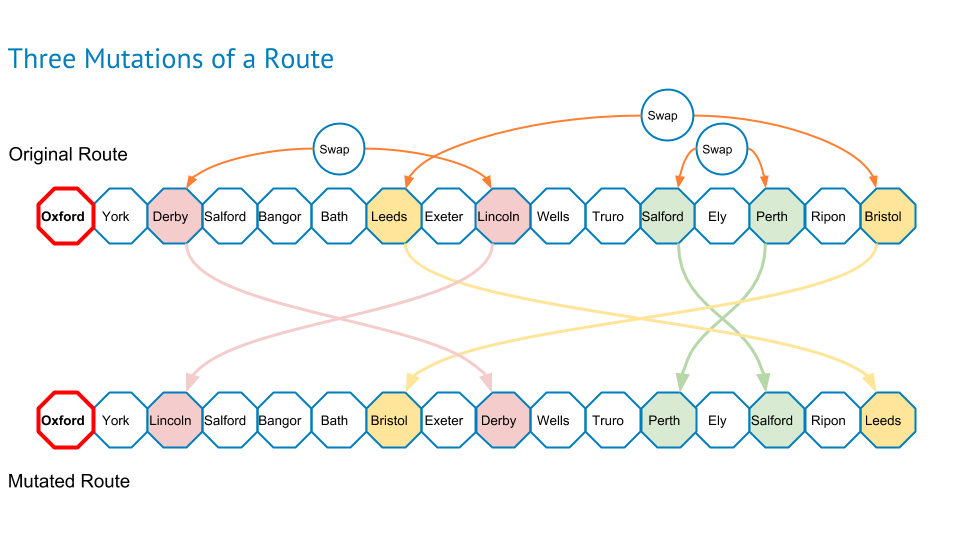
Procreation

Last on my list was some offspring to refresh the depleted population. And whilst I’m the father of five amazing children, I confess that this bit of the evolution soup caused me a few headaches. How could I sensibly share the characteristics of the parents to produce some offspring and do it in a way that was somehow true to Darwinian principles.

Anyway, back to procreation! (I don’t type that very often).

It was Love Island all over again and I considered limiting the “recoupling” to partners with similar levels of fitness, but in the interests of diversity, I donned the blindfold and started pairing them up randomly until I had enough “children!”

Now stay with me for this next bit because it hurt my head trying to work it out! (Or, if you’re not interested in the detail but are happy that I managed to code the procreation successfully, skip ahead to the bold red “phew!”.

I decided that I would have a father that would inject some elements of his route into the mother’s route. Within each pair, I allocated the mother role to the route that had the highest fitness.

The amount of route that the father would inject was a function of the parents respective fitnesses:

proportion_from_father = fathers_fitness / ( mothers_fitness + fathers_fitness)

And I decided that the injection would be in the form of pairs of cities that were next to each other in the fathers route.

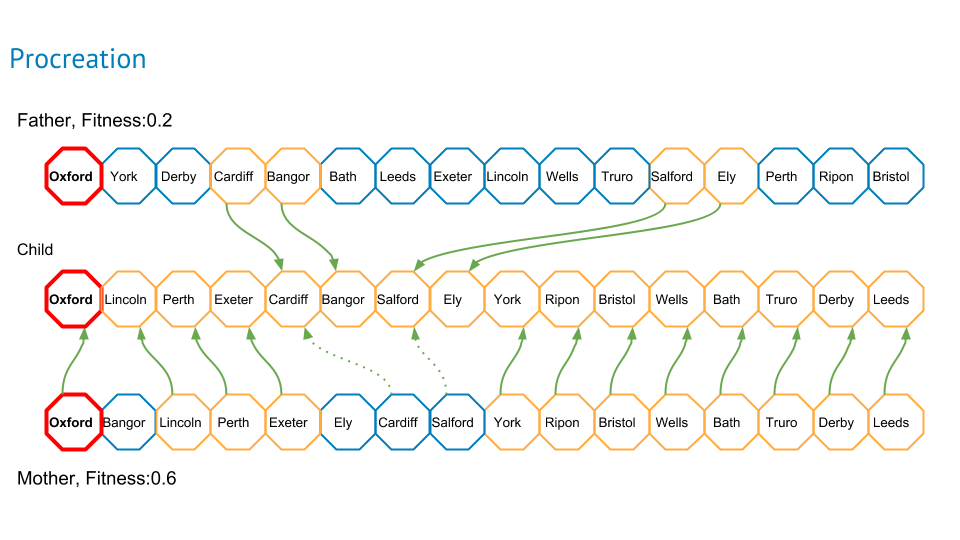
So I chose the correct amount of cities randomly and then took the city that was next to it in the father’s route. Sometimes, these pairs overlapped so a segment might not be just 2 cities.

Then I worked from the beginning of the mother’s route city by city. If the city wasn’t in the segments to be injected from the father then I copied it to the child. If the mothers city I was looking at was the same city as the first city in any of the fathers segments to be injected, then I stopped copying from the mother’s route and injected that segment from the father. Then I went back to the mothers next city and repeated until the child route was complete.

For a bit more diversity, I did some reversing as well. About 1/3rd of the time, I reversed the father’s route before the pairing, about 1/3rd of the time I reversed the mother’s route and the remainder I left the overall order as it was.

Phew!!!

Then I took the survivors, the mutations and the children and calculated the distances for all of them again and sorted into order.

Guess what happened next?

That’s right ? Rinse and repeat, just like in real life!

Each generation threw a new hero up the pop chart and the winning distance gradually got shorter and shorter.

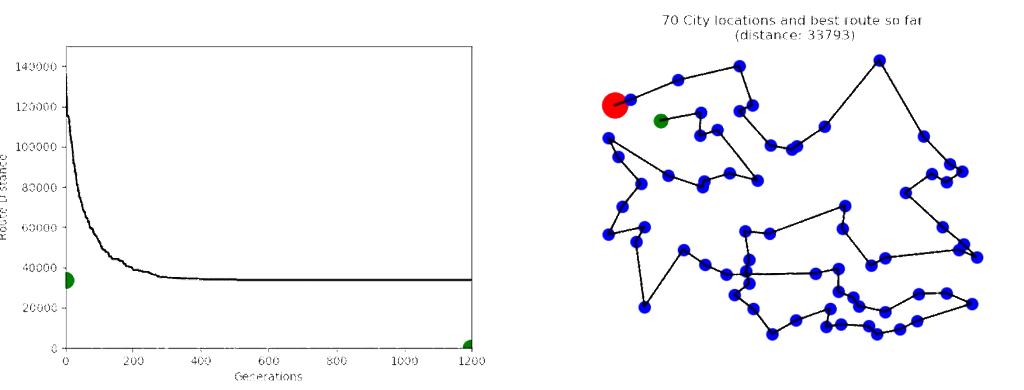
The route on the right was created after 2000 generational cycles and whilst it might be quite good, it’s not optimum. A good indicator of suboptimality (!) is when the route lines cross over each other. I’m reasonably sure the route is sub optimal if that happens.

And it can take a very long time to get to the optimum route, even for lower numbers of cities (say 25). In this example, we can see from the graph on the left that almost no improvement was made after about 500 cycles.

When I ran the evolutionary process with 70 cities as above, it never reached the optimum even after running for 24 hours.

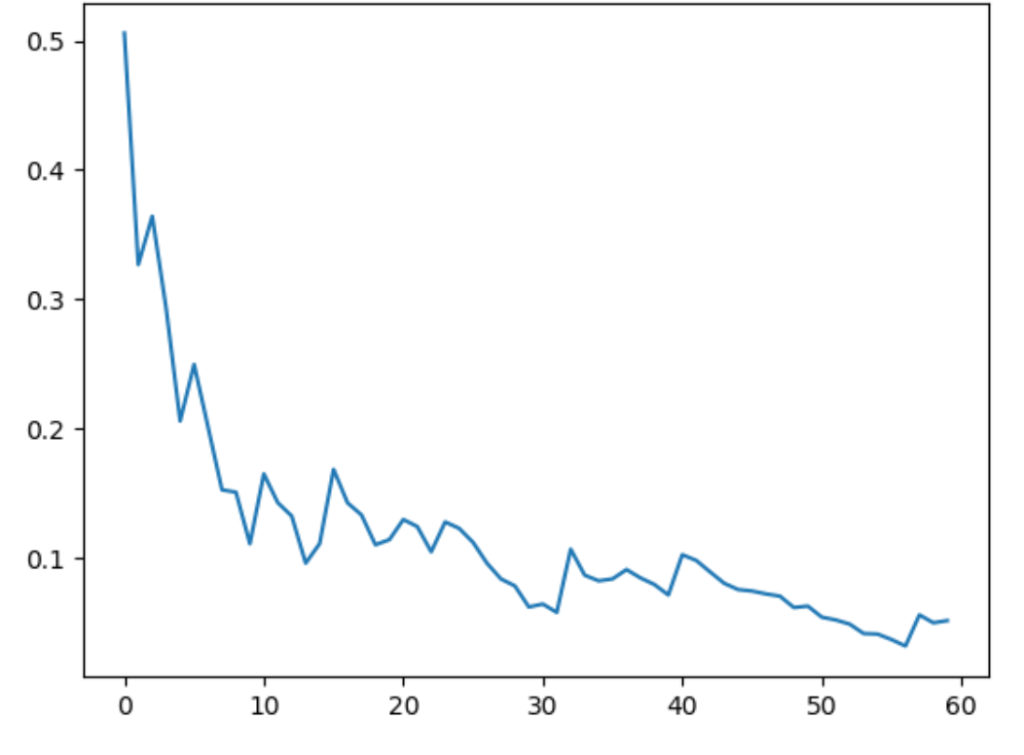
I looked at the collection of routes and found that after a while, they were all very similar and diversity in my pool of routes was rather low. I tried a number of things to increase that diversity but had only limited success.

The following chart shows the sharp decline of diversity (y axis) as the number of iterations increases (x  axis) over a very small number of iterations.

In the natural world, mother nature has some behaviours that could help me. As creatures evolve, they can find themselves divided into independently evolving groups that are separated by physical barriers such as a range of mountains, or an ocean for example. Eventually, one or more of the groups may become fit enough to swim the ocean or cross the mountains and the diversity of genes is increased.  

I tried to replicate this process in my model by forming a number of independent route pools and then leaking the best routes across the pools after a set number of iterations.

I stacked the videos of route progression for each route pool on top of each other and you can see the results in the two minute video here (if you can maximise the video to run full screen, I’d definitely advise it):

The best route that I found across all the runs I did (many, many, many runs!!) is here:

Winning route ancestry

I was interested to know what processes the winning route had been through to end up as the shortest one found, so I stored every evolutionary event (survival, birth, mutation, leaking)  and created this visualisation with a vertical stripe appropriately coloured for each of the iterations.

For the children, I copied over the ancestry of the mother as that one had most of its route carried forward into the child.

There is a key to show the different meanings of the lines below:

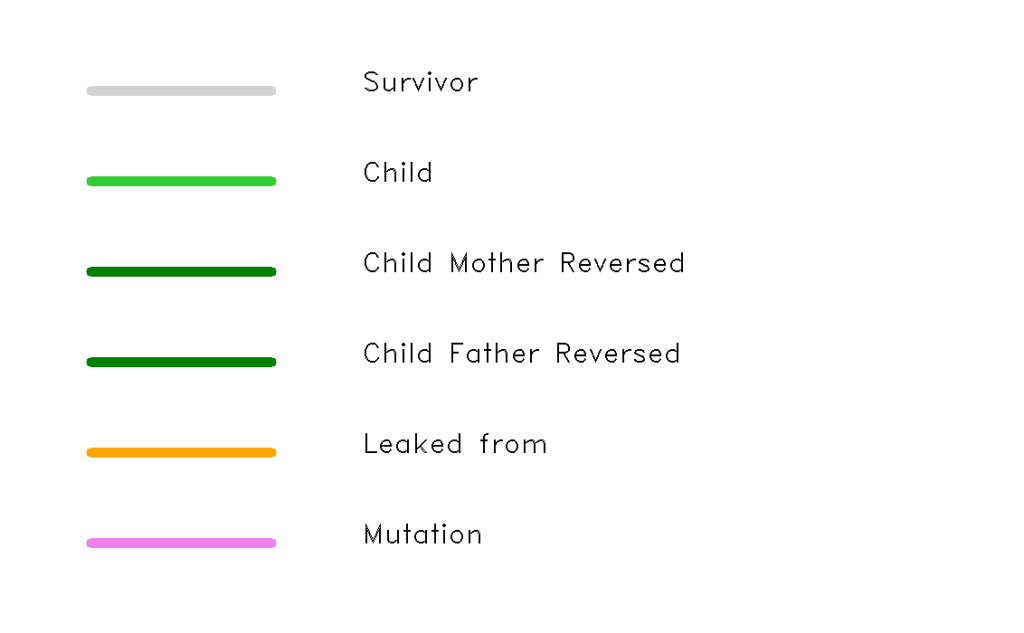
It’s quite hard to see the detail on this picture, but if you click on it, then you can see more clearly.  Throughout the history of this route, successful mutations are not very common and in fact, only two occurred. One early on and one very late. It was the late one that led to 4 further successful procreation and then the shortest route was achieved.  So, the successful random variations may be quite rare, but in this instance, it had a dramatic effect. 

It doesn’t tell us if any of the fathers were successful mutations or children of routes that leaked over from the other pools as I couldn’t think of a clear and concise way of showing that information. It’s the lineage on the mother’s side only.

Technical Reflection

The multi route pool strategy was successful in improving the best route found but it increased the run time, the number of choices to make and parameters to optimise:

• How many route pools should I have?
• How many iterations should I run before leaking the best routes across the route pool boundary?
• How many times should I run the leak / iterate cycle?
• How do the answers above vary as the number of cities increases?

It would be fun(!) to automate that process of exploration and find the best answers.

Another area for me to dig into further is the speed optimisation. In general, my approach on these personal learning projects is to optimise the smallest amount needed so that the run times don’t annoy me!

By the time I’d concluded my project, that test was stretched to the limit!

To run a single evolutionary cycle for 70 cities with 2000 routes in the pool takes about 1.1 seconds. It might not sound like much but if you have five route pools, and want to run 1000 iterations, then it’s about 90 minutes.

Whilst I was pretty happy with the progress I made on this problem, it’s a long way short of the best results in the field. Wikipedia tells me that in 2006, the Concord program calculated the optimal route for 85,900 cities. It’s the largest map solved optimally so far.

If you’re satisfied with a route that’s guaranteed to be within 3% of the optimal, then there are solutions available that can calculate a good route for millions of cities! Human endeavour is utterly astonishing!

But the thing that’s troubling me the most is a bit harder to explain. Whilst I didn’t read any more about it when I was coding, I did know that using Darwinian ideas would lead me to a solution. It was like an exam question. Real life isn’t always like that and being skilled at finding good ways to solve hard problems in an uncertain world is a valuable skill.

If you’d like to have a look more closely at my solution, you can see all the code on my personal github page

General Reflection

I’ve used Darwinian thinking many times in the last 30 years to help solve many business problems, but I’ve never coded a solution up from scratch for a purely numerical problem. I’m really glad that I did and I learned a huge amount while completing my own ridiculous challenge!

Neural nets (especially convolutional ones) are all the rage and definitely the plat du jour in ai circles.

However, I found riches in the less traveled roads such as genetic algorithms and reinforcement as in my previous blog.

I’m still astonished that this problem can be solved pretty well using ordinary techniques that try to mimic the evolution of life in the real world.

And if the solving of this problem, seems a bit removed from real life then it might be worth taking a moment to think about a couple of things.

• Firstly, how is the travelling salesperson problem like other problems that any of us might experience in our personal and business lives?
• Secondly, what other problems could lend themselves to some Darwinian thinking?
  • For example, if a problem solving process is stuck, could it help to:
    • Change the context
    • Look for ocean crossing solutions from nearby domains
    • Increase diversity of the potential solution pool by inviting some new players to help think about it
    • Randomly remove some of the constraints for a while.
    • Try combining some of the existing solutions to see if something new can be synthesised
    • Etc!

When we practise those thought exercises, we get more skilled at jumping solutions from one domain to another and that is one of the five pillars of innovative thinking that I’ve written about before.

If you have any problems that you think might benefit from some Darwinian thinking, give us a call!